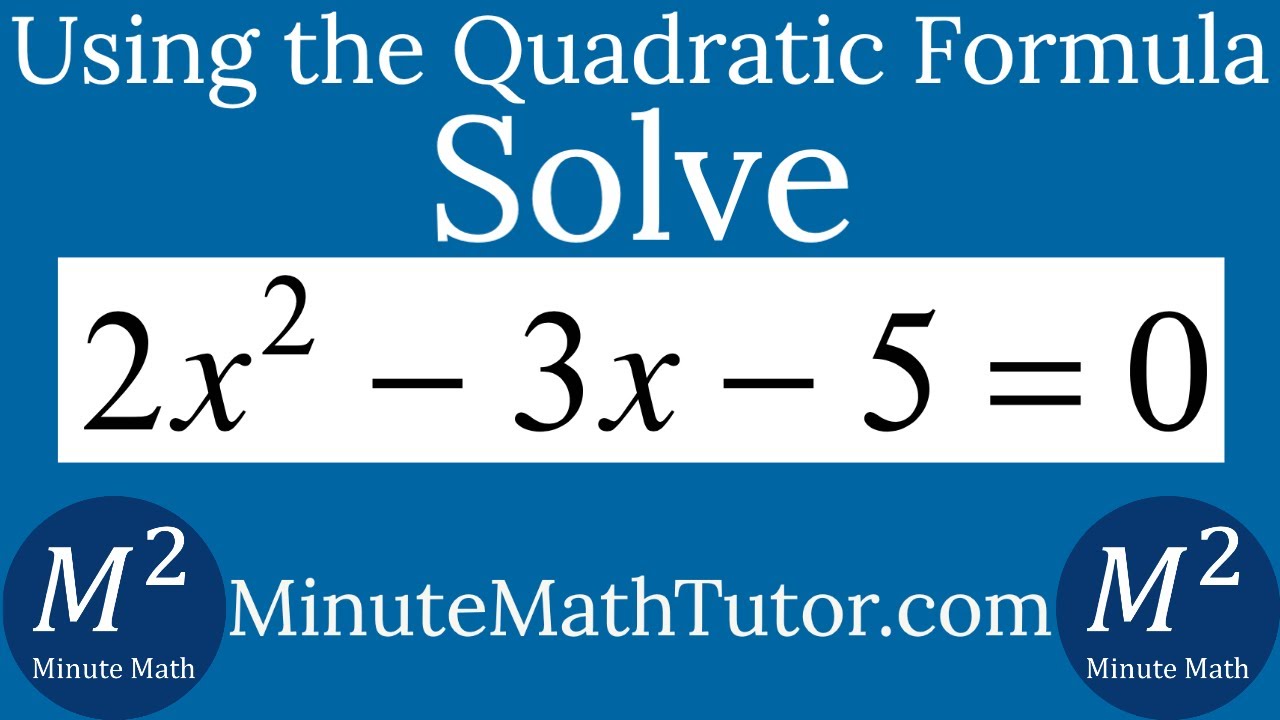In the world of mathematics, equations are the building blocks of problem-solving. One such equation that often challenges students and mathematicians alike is the quadratic equation. In this article, we will delve into a specific quadratic equation: 2x^2 – 3x – 5 = 0. We’ll break it down, explore its roots, and discuss its real-world applications. By the end of this journey, you’ll have a comprehensive understanding of this quadratic equation and its significance.
What is a Quadratic Equation?
Before we dive into the specifics of 2x^2 – 3x – 5 = 0, let’s briefly recap what a quadratic equation is. A quadratic equation is a second-degree polynomial equation, meaning its highest power of the variable is 2. The general form of a quadratic equation is:
ax^2 + bx + c = 0
Here, ‘a,’ ‘b,’ and ‘c’ are coefficients, and ‘x’ represents the variable we’re solving for. In our case, ‘a’ is 2, ‘b’ is -3, and ‘c’ is -5.
Solving 2x^2 – 3x – 5 = 0
Step 1: Identify the Coefficients
In our equation, 2x^2 – 3x – 5 = 0, ‘a’ is 2, ‘b’ is -3, and ‘c’ is -5. These coefficients are crucial in solving the equation.
Step 2: Use the Quadratic Formula
The quadratic formula is a powerful tool for solving quadratic equations:
x = (-b ± √(b² – 4ac)) / (2a)
Step 3: Calculate the Discriminant
The discriminant, given by ‘b² – 4ac,’ plays a significant role in determining the nature of the roots.
Step 4: Find the Roots
Depending on the value of the discriminant, we can classify the roots into three cases:
Case 1: Discriminant > 0
In this case, there are two distinct real roots.
Case 2: Discriminant = 0
Here, we have a single real root with multiplicity.
Case 3: Discriminant < 0
This case results in complex roots, which are conjugate pairs.
Real-World Applications
Quadratic equations find their applications in various fields, including physics, engineering, economics, and even in our day-to-day lives. Some common scenarios where quadratic equations come into play include:
- Projectile Motion: Calculating the trajectory of a thrown object.
- Structural Engineering: Analyzing the strength and stability of structures.
- Finance: Modeling investments and loan amortization.
- Optics: Designing curved mirrors and lenses.
Conclusion
In this article, we’ve explored the quadratic equation 2x^2 – 3x – 5 = 0. We’ve learned how to solve it using the quadratic formula, discussed the significance of the discriminant, and touched upon real-world applications. Equipped with this knowledge, you can now tackle quadratic equations with confidence and apply them to solve real-life problems.