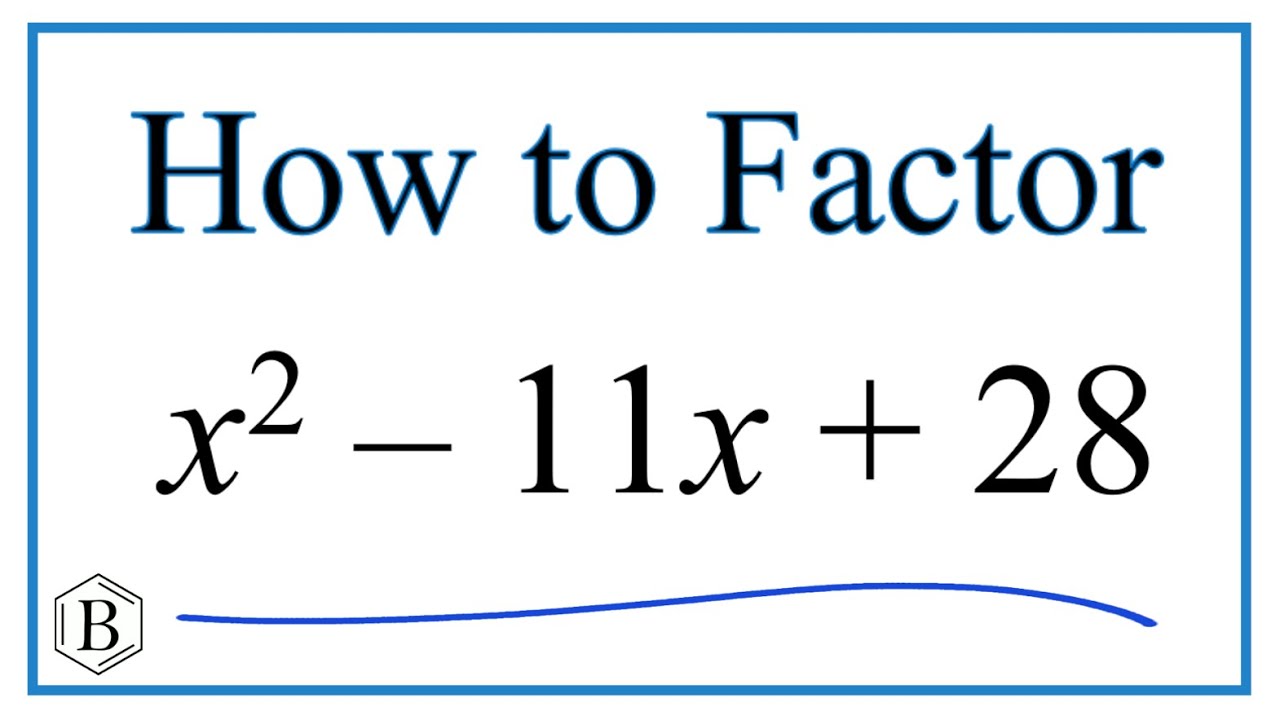Quadratic equations hold a significant place in the realm of algebra and mathematics x2-11x+28=0, as they frequently appear in mathematical problem-solving and real-world scenarios. In this comprehensive article, we will delve deeply into the quadratic equation x2-11x+28=0. Our journey will encompass understanding its roots, applying factoring methods, exploring graphical representations, and uncovering practical applications. By the end of this exploration, you will have a profound grasp of how to solve, interpret, and utilize such equations effectively.
What Constitutes a Quadratic Equation x2-11x+28=0?
Before we embark on deciphering the specifics of our equation, let’s take a moment to revisit the core concept of quadratic equations. A quadratic equation is a polynomial equation of the second degree, typically represented in the form ax^2 + bx + c = 0. Here, ‘a,’ ‘b,’ and ‘c’ are constants, while ‘x’ stands as the variable we aim to solve for.
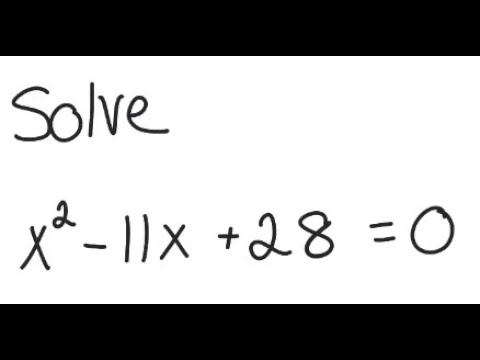
Factoring the Equation: A Methodical Approach
To unlock the solution to the quadratic equation x2-11x+28=0, we will employ the method of factoring, which is a fundamental technique used to deconstruct complex equations into simpler components.
Step 1: Identifying the Coefficients
Our equation presents ‘a’ as 1, ‘b’ as -11, and ‘c’ as 28. The first step in factoring involves finding two numbers whose sum equals the coefficient of ‘x’ (in this case, -11), and whose product equals the constant term ‘c’ (which is 28).
Step 2: Discovering the Factors
Through careful consideration, we identify that the two numbers which satisfy these criteria are -7 and -4. This is because the sum of -7 and -4 is indeed -11, and their product equates to 28.
Step 3: The Act of Factoring
With our numbers in hand, we can proceed to factor the equation, which results in the following expression:
(x – 7)(x – 4) = 0
Step 4: Solving for ‘x’
To ascertain the values of ‘x,’ we set each factor equal to zero:
- x – 7 = 0
- x – 4 = 0
Upon solving these equations, we attain the following solutions:
- x = 7
- x = 4
Thus, we have successfully determined that the roots of the quadratic equation x2-11x+28=0 are x = 7 and x = 4.
Also Read: 2×2-3x-5 = 0 Solution
Visualizing the Equation: Graphical Representation
Understanding the graphical representation of quadratic equations provides us with valuable insights into their behavior and characteristics.
The Elegance of Parabolic Curves
Quadratic equations, when graphically represented, manifest as parabolic curves. In the specific case of x2-11x+28=0, the curve exhibits a graceful U-shape, opening upwards. The vertex of this parabola represents the minimum point on the curve.
Practical Applications
Quadratic equations find relevance and application in a myriad of fields, spanning from physics and engineering to economics and biology. One of their most prevalent uses can be observed in the realm of projectile motion calculations, where the path of a projectile follows a quadratic trajectory.
Conclusion
In conclusion, our journey has led us through the intricate world of the quadratic equation x2-11x+28=0. We’ve uncovered the art of factoring, discovered its roots, and visualized its parabolic nature. Quadratic equations are more than just mathematical abstractions; they play a vital role in various scientific and engineering domains.